上一次我们分析了wti原油和布伦特原油的双品种套利模型，那么我们常见的几个直盘货币对之间是否也有联动性呢？这次我们依然使用线性回归和非线性回归同时来研究一下这个问题。

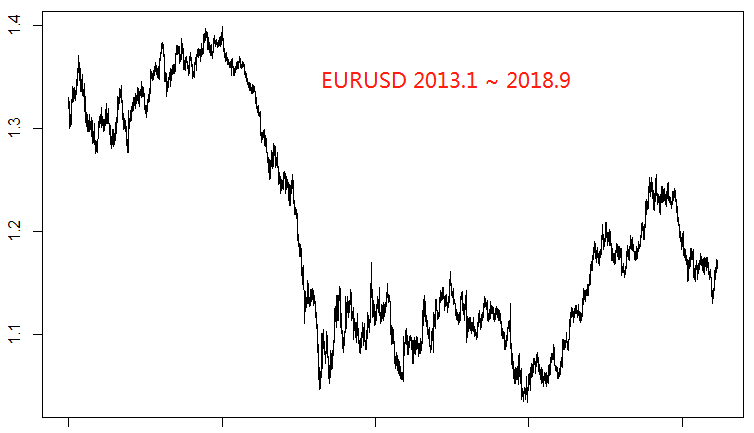
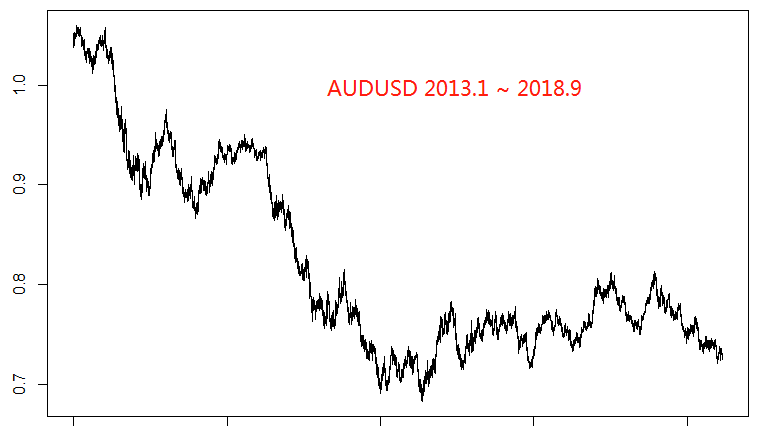
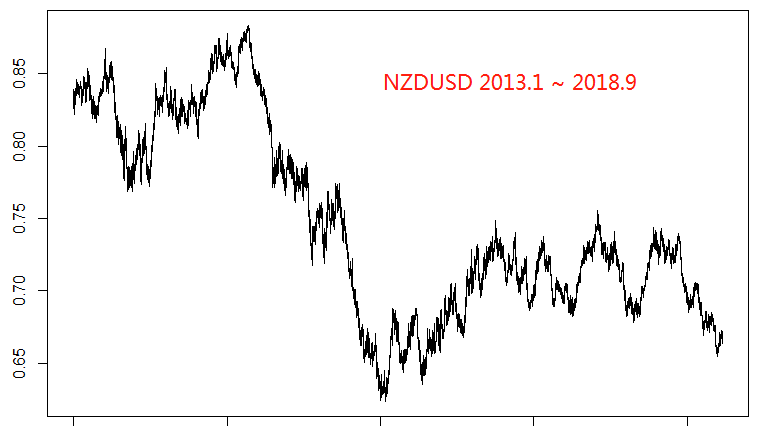
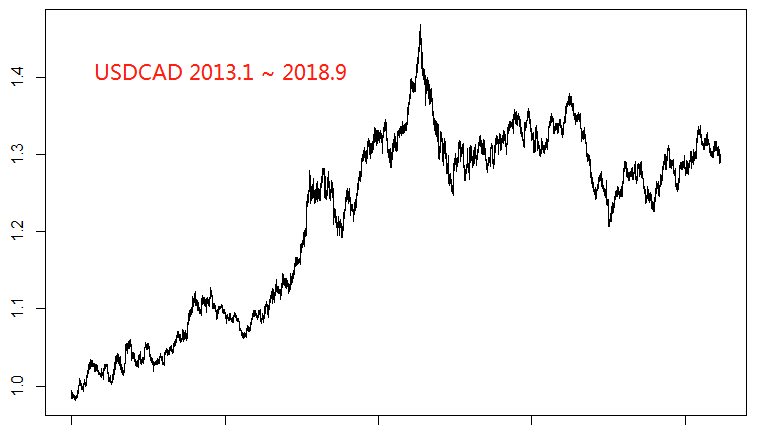
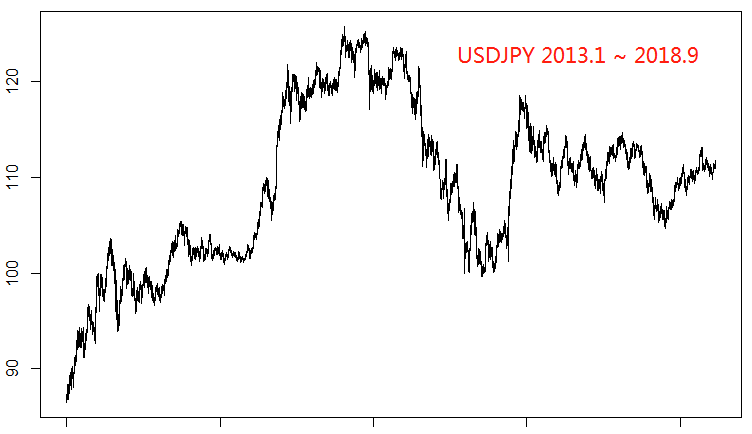
         我们使用的五个直盘货币对是EURUSD，AUDUSD，NZDUSD，USDJPY和USDCAD。首先我们来看一下他们各自的走势：

         ① 线性回归

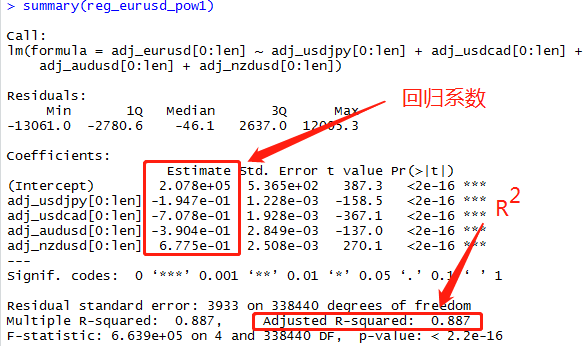
         以EURUSD作为因变量，其它四个货币对作为自变量，使用前4年的数据作为训练集，最后一年的数据作为测试集，得到回归结果如下：

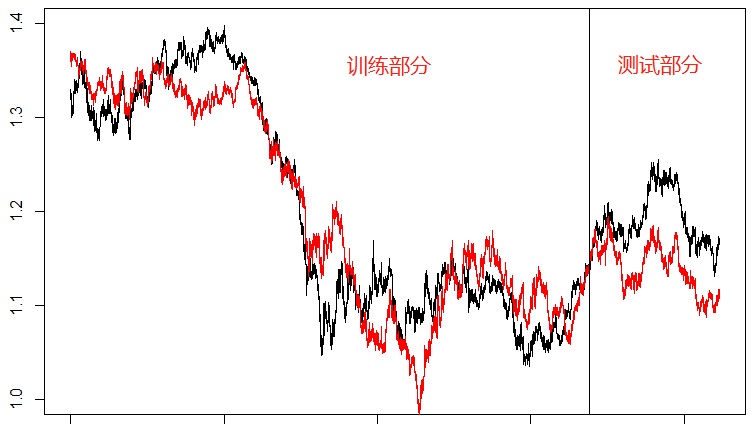
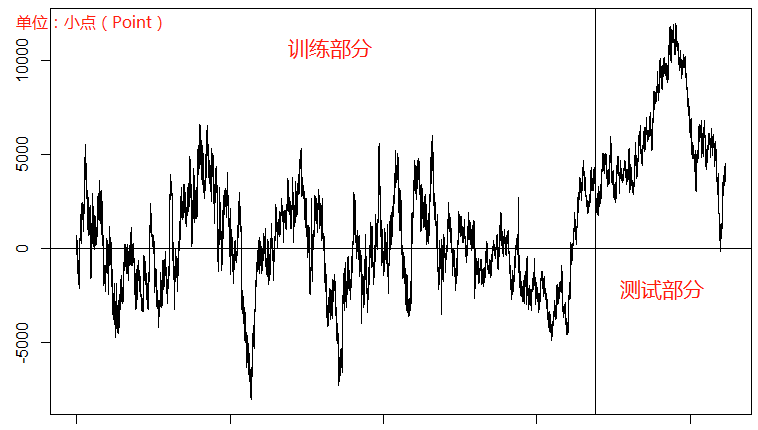
残差图：

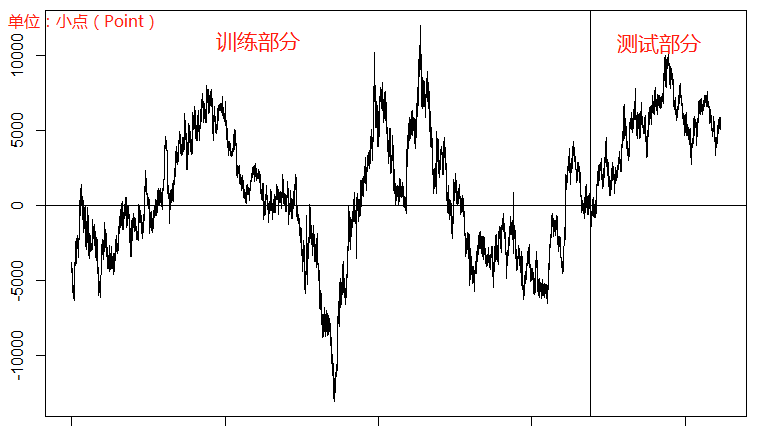
         我们回归套利的本质就是根据历史价格的规律总结，配置一个资产组合，使得这个组合的走势和残差图完全一致，当残差偏离零轴很多的时候，就有回归零轴的需求，如果此时残差大于零，我们就做空这个组合，如果残差小于零，我们就做多这个组合，当残差回归到零轴的时候，回归的这些点数，就是我们这个组合的整体收益。

         如果残差回归的频率越高，代表我们的交易机会越多，如果我们从残差偏离很远的地方进场回到零轴，我们收益的点数就越大。当行情改变，残差不再回归零轴时，我们则需要止损，并重新计算模型，或者放弃此模型。

         从上面的残差图上就可以看出来，残差回归的频率很低，而且偶尔可能偏离零轴过远（1000个大点以上）。再看预测部分的残差，一次也没有回归过，所以这五个直盘货币对的关联性可以说是比较低了，不适合用这个模型来做套利。

         ② 非线性回归

         开头说过这次除了线性回归，还要用到非线性回归的方法。线性回归类似拟合一个y = ax + b的函数式，这里只用到了自变量x的一次方作为影响y的因子，那y有没有可能和x的平方或者立方等等成线性关系呢？这时就需要用到非线性回归了。

         我们假设：eurusd = a0 + a1 * audusd + a2 * nzdusd + a3 * usdcad + a4 * usdjpy + a5 * audusd^2 + a6 * nzdusd^2 + a7 * usdcad^2 + a8 * usdjpy^2

         然后我们依然是把数据拆分成训练集和测试集，以下是回归的结果：

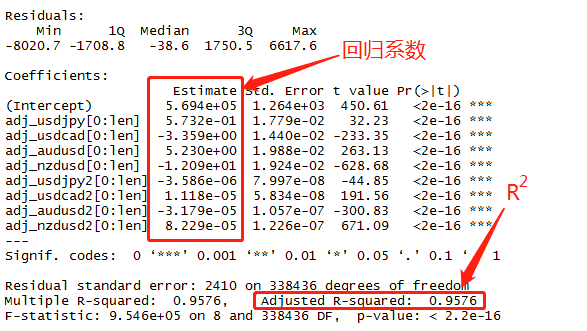
         可以看到R2比一阶回归的R2要高了许多，R2是线性回归中的决定系数，取值范围在0~1之间，R2越接近1说明整体的回归效果越好。但是一般来说，自变量的数量越多，R2自然也会越高，我们这里相当于是直接增加了4个自变量，所以R2显著提高也是在预料之中的，接下来我们看一下回归图和残差图。

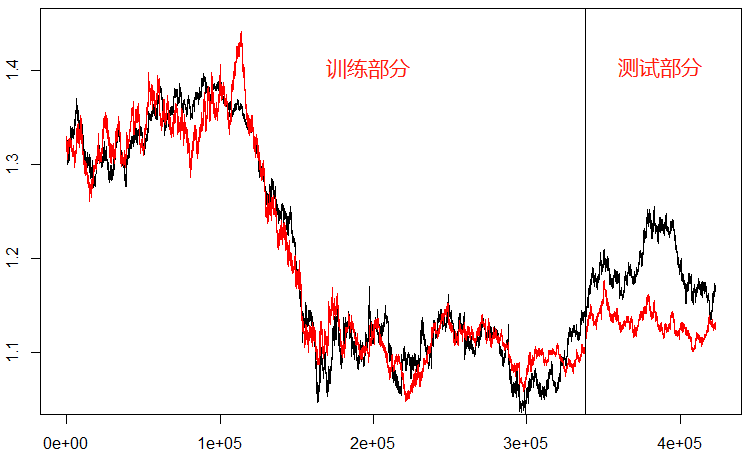
残差图:

         这里明显看到在训练集的部分，红色的预测曲线和黑色的实际历史走势“贴合”的更好了，这一点和R2的增加是一致的。但是在测试部分红色曲线和黑色曲线相差甚远，残差图也未能保持之前的回归频率，所以纯粹的提高自变量的阶数带来的可能只是过度拟合，并不能给我们更好的预测模型。

         这个结果也能间接说明各个直盘货币之间的联动性其实并没有那么强，基于四种货币的价格信息是无法预测第五种货币的。从基本面上来看，就算全世界大的经济周期基本保持一致，每个国家的货币政策和财政政策也都不一样，这才导致不同的货币存在不同的货币属性，既然属性都不一样，怎么会有很强的联动性呢？对吧。