在之前的文章中，我们研究了货币对之间和两油之间的相关关系，那么各国股指之间存在同样的线性关系吗？我们分别下载了标普500指数（SPX500）、德国30指数（GER30）、日经225指数（JPN225）和香港恒生指数（HSI）。
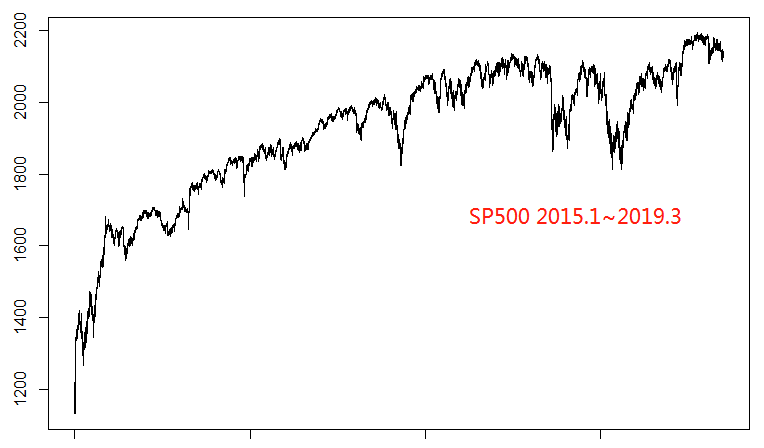
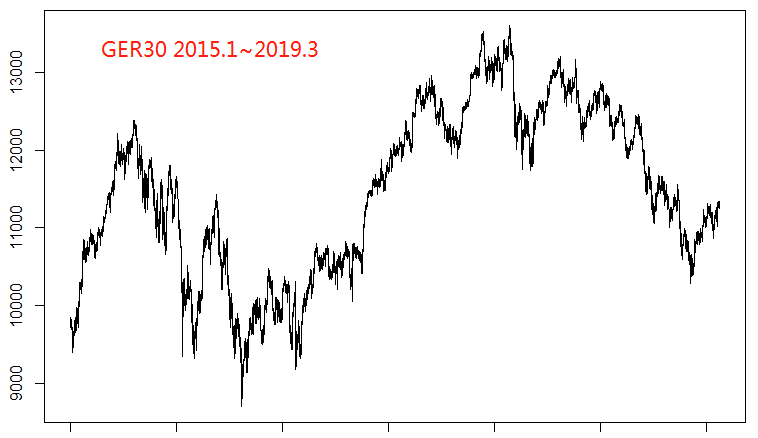
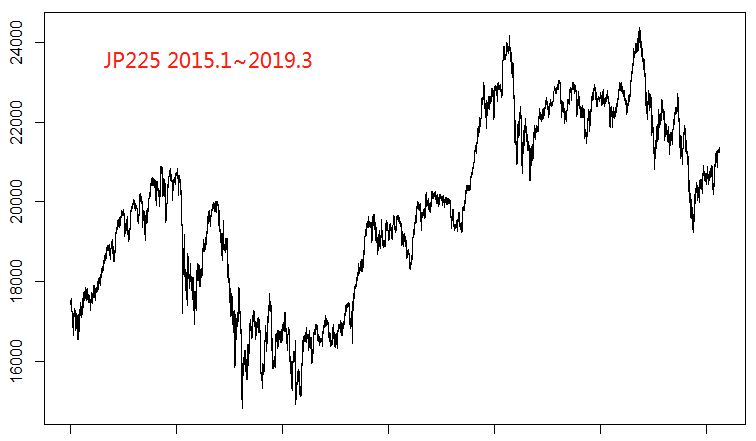
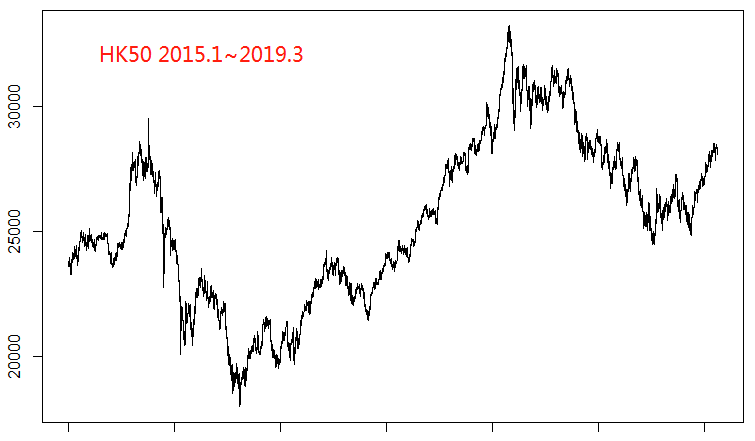
从图上可以看出这几个股指在过去4年的大致走势：SPX500先是一路高歌猛进，然后在高位盘整；而GER30、JP225和HSI都可以用跌涨跌来大概描述这几年的走势。
构建股指对冲模型
这里我们选取德指、日经和恒生指数这三个品种，分析他们之间的相关性。按照惯例，我们还是先来看看散点图，由于是三个品种，所以散点图依然是三维立体的。我们用一个视频来展示三个股指的空间分布情况。
（视频无法正常播放请点击这里 ）
一般来讲三维空间总线性回归的目标是找到合适的参数a、b、c使得Z = a*X + b*Y + c，这个式子表示的是一个空间中的平面，但是从上图看，这三个品种的散点图构成的形状更像是一个“枣核”，那么我们可以考虑使用一条空间中的直线来回归此模型。
残差图
这样的回归模型比较少见，我们也只在Matlab里找到了对应的回归方法和函数。我们使用空间中的两个点来表示这条直线，分别是（18887,15642,9560.9）和（31977,24008,13390）。然后再用空间点到直线的距离公式计算每个对应的点的残差，画出残差图：
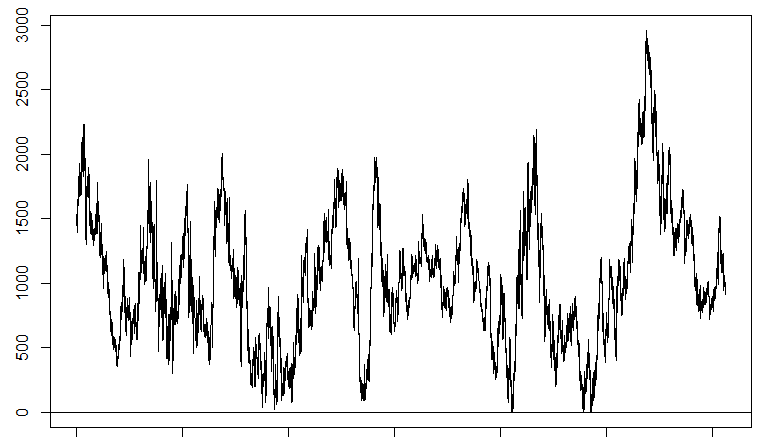
这个残差图和之前的不太一样，之前的残差是在零轴上下来回波动，这里的残差对应的是空间中的距离，距离是一个非负数，所以残差的波动范围是在[0，+∞)，此图中的残差大多数情况都在2200以下，最高也没有超过3000，这个残差相对还是比较稳定的，而且上下来回震荡的频率也比较高，我们就可以设计一个策略，当残差到达1500~3000的时候建立投资组合向轴心去回归进场，当残差回到500~800的时候获利了结。
三个品种建仓的方向和手数大小是由空间点垂直到空间直线的单位方向向量决定的，这里有一点要注意的是，我们模型中是按照空间直线去回归的，但是在我们入场的那个时刻，实际上我们还是以平面去回归的，这个平面的单位法向量就是上面提到的空间点垂直到空间直线的单位方向向量。
有趣的优势
如果你对解析几何和向量空间还有印象，而且上面这段话你也看懂了的话，下面我们将介绍这个模型最精彩也最有意思的地方：
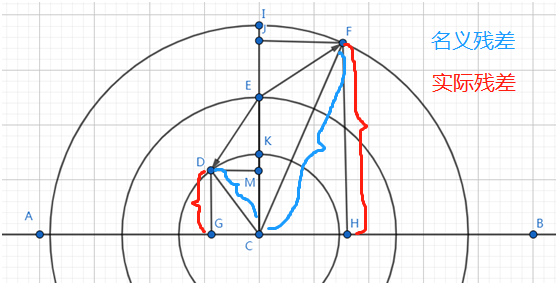
上图中如果我们沿着这条回归直线的方向来观察这个体统，那么这条回归直线在我们看来就是一个点了。这里我们假设点C就是我们的回归直线，点E是我们进场时价格所在的位置，进场之后我们沿着向量EC的方向建仓，等待残差回归，在建仓的这一时刻我们可以说是朝着垂直于回归直线C的方向，也可以说是朝着垂直于平面AB的方向去回归，因为这两个向量是同方向的。这一点弄清楚之后，我们来看当价格发生改变之后，我们会面临什么情况。
①、当散点从点E移动到了点F，我们的残差（或者叫名义残差，表示散点到回归直线的距离）就从CE的长度变成了CF的长度，又因为CF = CI，名义残差的变化量则为EI，然而我们的持仓方向是向量EC的方向，此时我们实际的残差应该是点F到平面AB的距离FH，又因为FH = JC，我们的实际残差（持仓实际增加的浮亏）的变化量应该为EJ，也就是说当残差在增加的时候，名义残差是大于等于实际残差的，也就是我们账户实际浮亏的金额要比名义残差的变化量要小。
②、当散点从点E移动到了点D，我们的名义残差就从CE的长度变成了CD的长度，又因为CD = CK，名义残差的变化量则为EK，然而我们的持仓方向是向量EC的方向，此时我们实际的残差应该是点D到平面AB的距离DG，又因为DG = DM，我们的实际残差（持仓实际增加的浮亏）的变化量应该为EM，也就是说当残差在减小的时候，名义残差是小于等于实际残差的，也就是我们账户实际浮盈的金额要比名义残差的变化量要大。
总结一下就是我们亏钱的速度比残差放大的速度要慢，赚钱的速度比残差收敛的速度要快，无论残差怎么变化，我们的持仓总是相对有优势的。这就是这样一个空间直线模型的优势。
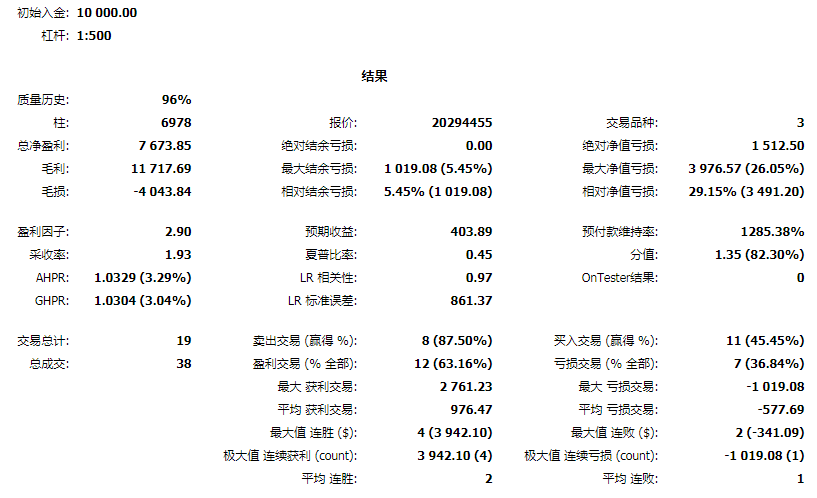
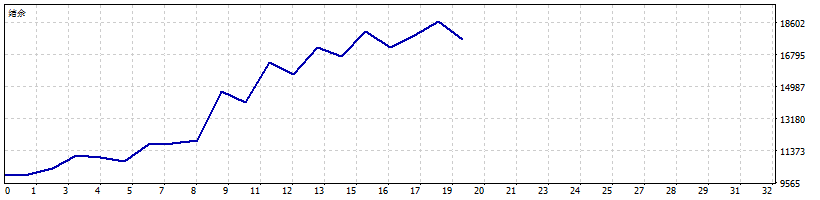
我们把这个策略写成了ea在mt5中进行了回测。按照惯例，我们还是不选取最优参数展示，只找一组普通的参数来做一个展示策略的回测效果：我们看到：回测时间段2018.1~2019.3，收益率76%，最大净值回撤26.05%。这样的风险收益比还是比较让人满意的。
究
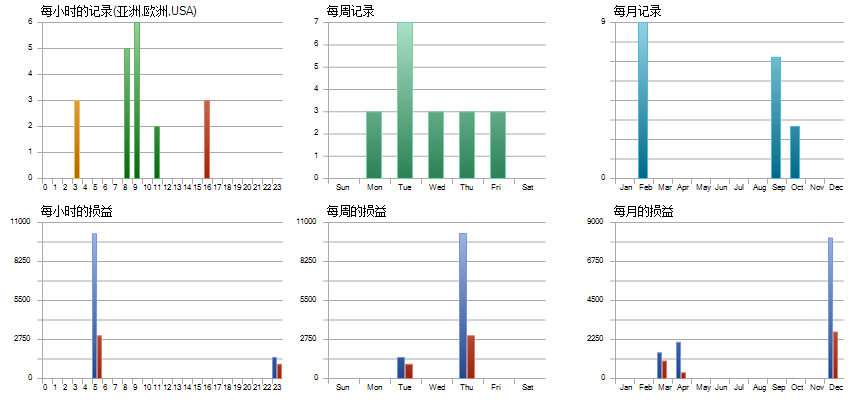
点击这里可以看到详细的交割记录
发表评论