前面和大家介绍了这么多关于回归的对冲模型。 之前的研究报告传送门:
今天我们再来研究一下,如何基于金银铂钯这四大金属的商品属性,设计一个套利策略呢?照旧先来看看这四个贵金属的历史走势图吧:
黄金(XAUUSD)
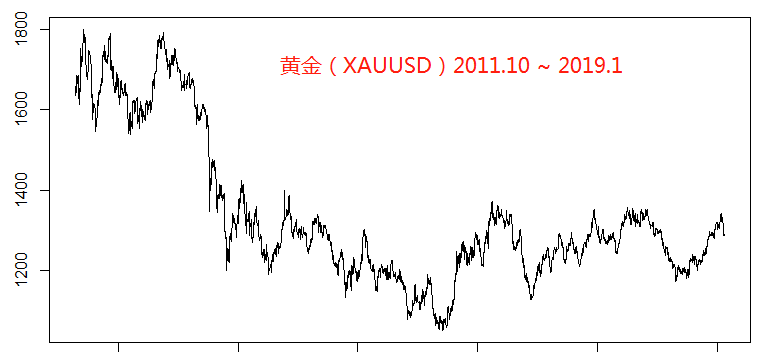
白银(XAGUSD)
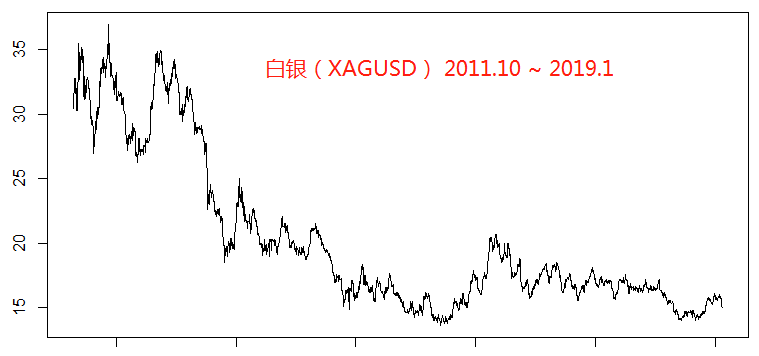
铂金(XPTUSD)
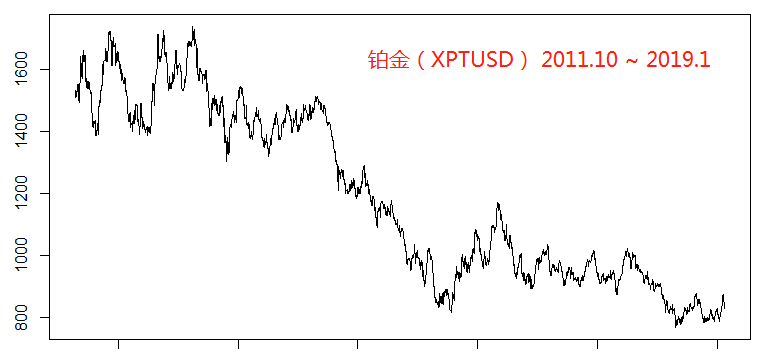
钯金(XPDUSD)
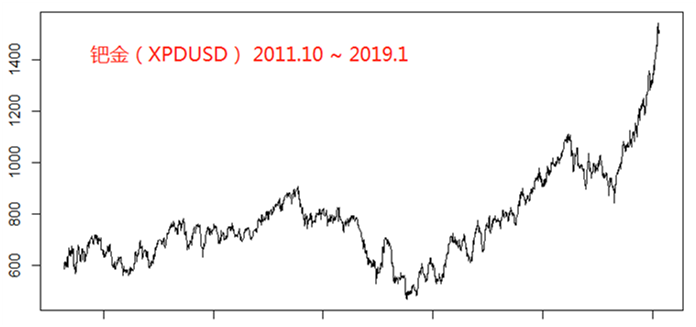
乍看上去金银铂的走势比较类似,都是震荡下行,但是钯金的走势却恰恰相反一路高歌。那么可能有人会问了,既然走势差这么多,你还把钯金也包含进来去回归,效果是不是会更差呢?这个问题我们在后面也会拿出具体的结论给大家一个论证,也会从理论的角度做一个分析。
话不多说,直接以黄金为因变量,另外三个贵金属为自变量,我们来看看回归的结果:
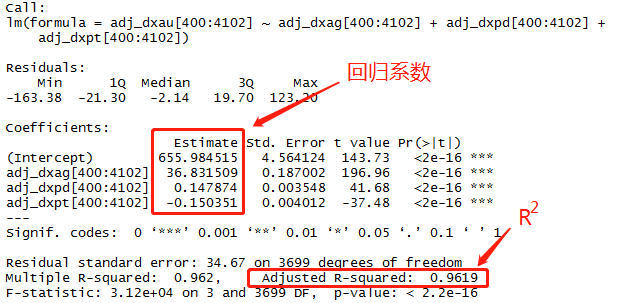
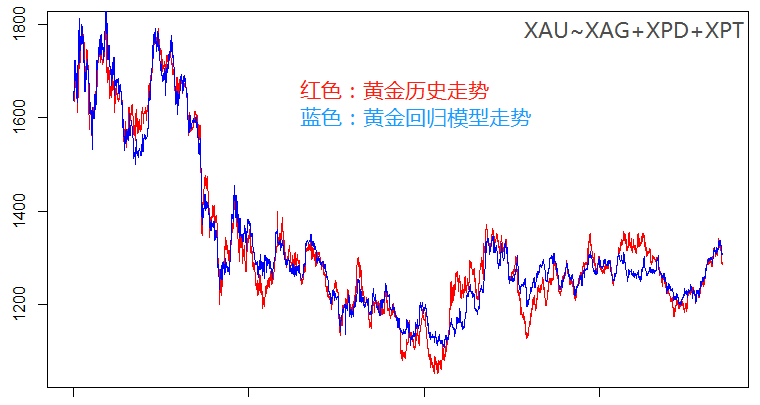
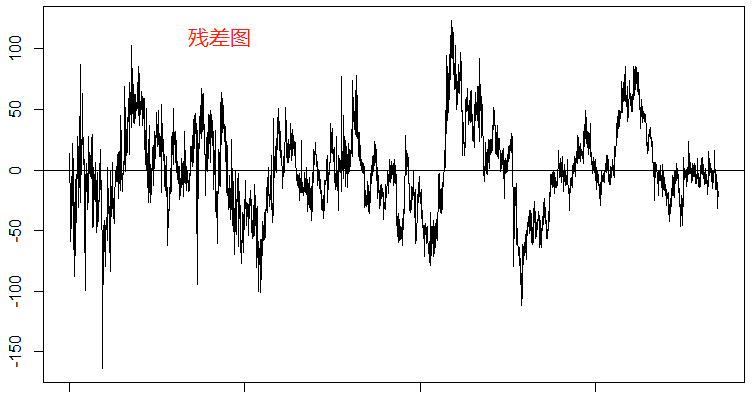
就模型而言0.96的均方误差可以说是拟合度非常好了,从模型走势和真实走势的对比图上也能看出来个大概。整体的残差而言偏离的幅度较大,最大幅度超过了150美金,对于黄金而言就是1500个标准点(大点);但是残差回归零轴的频率还是很高的, 针对这种模型,我们必须要等到残差偏离较大的时候再进场,这样可以更好的控制风险。
那么接下来我们来试一下去掉钯金(XPDUSD)之后的回归情况又如何呢?
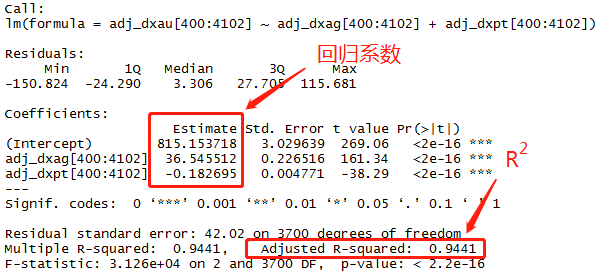
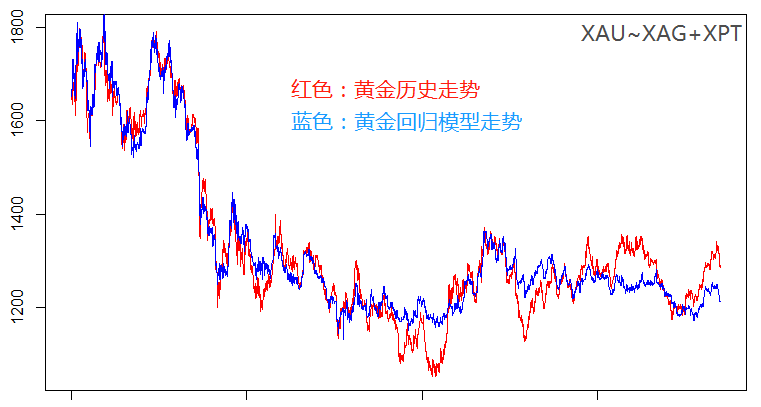
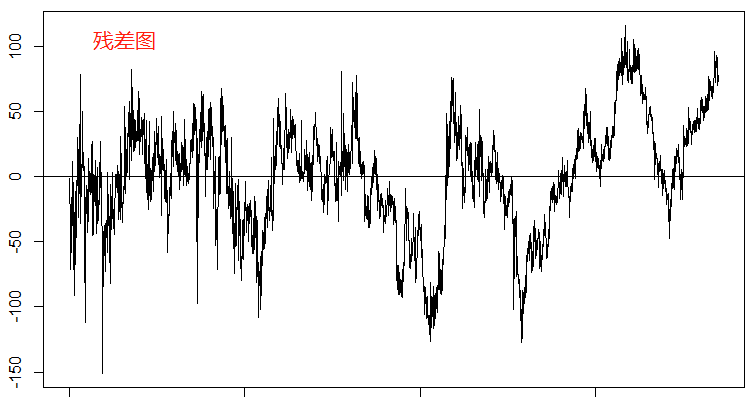
肉眼上看模型和残差的整体表现和四个品种一起回归的效果相差不大,但是三品种的模型近期的残差回归频率是在不断降低的,也就是说可能有失效的趋势。
其实这里我们可以反过来看这两个个模型回归的顺序,我们先用了两个变量(白银的价格和铂金的价格)来预测黄金价格的走势,然后发现均方误差还挺高,但是这个残差回归的频率在逐渐降低,然后我们再多引入了一个品种钯金(XPDUSD),乍一看,这个钯金的走势和其它三个品种的走势大相径庭,但是我们还是毅然决然的把他加入到了我们回归的模型当中去了,然后结果我们发现均让误差比以前要更好了一些,残差的回归频率也相对更稳定了,其实这并不奇怪,因为我们在研究相关性的时候除了正相关行以外还有负相关性,也就是A的价格上涨会导致B的价格下跌,这里我们从回归系数也能看出来,钯金的回归系数是个负数,这就是他和黄金价格呈负相关性的体现。
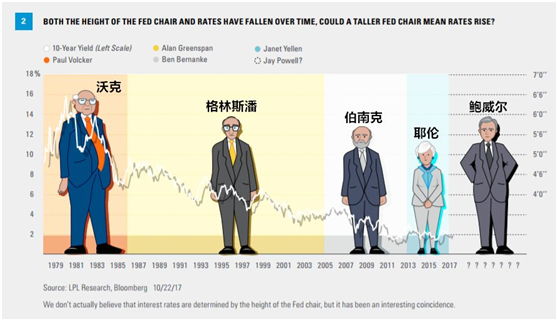
这里再补充两点:第一点是,当我们在做回归模型的时候,其实只要去添加自变量的个数,回归的拟合程度都会多多少少有提升,因为几乎不存在两组数据之间的相关性为0的情况,只要有一点点相关性,就能或多或少的提高整体的拟合程度。第二点是,单纯数值上的表现往往不足以说明问题,背后的逻辑才是整个回归模型的理论支撑。打个比方吧,曾经就有人拿美联储主席的身高和美国的利率来做统计回归,如上图所示,是不是感觉很玄学呢。但是这些可能往往只是一些巧合恰好碰到一起了,我们也把这种现象叫做丁蟹效应。大家在做其他事情的时候也千万不要被一些表面的数字所误导了。
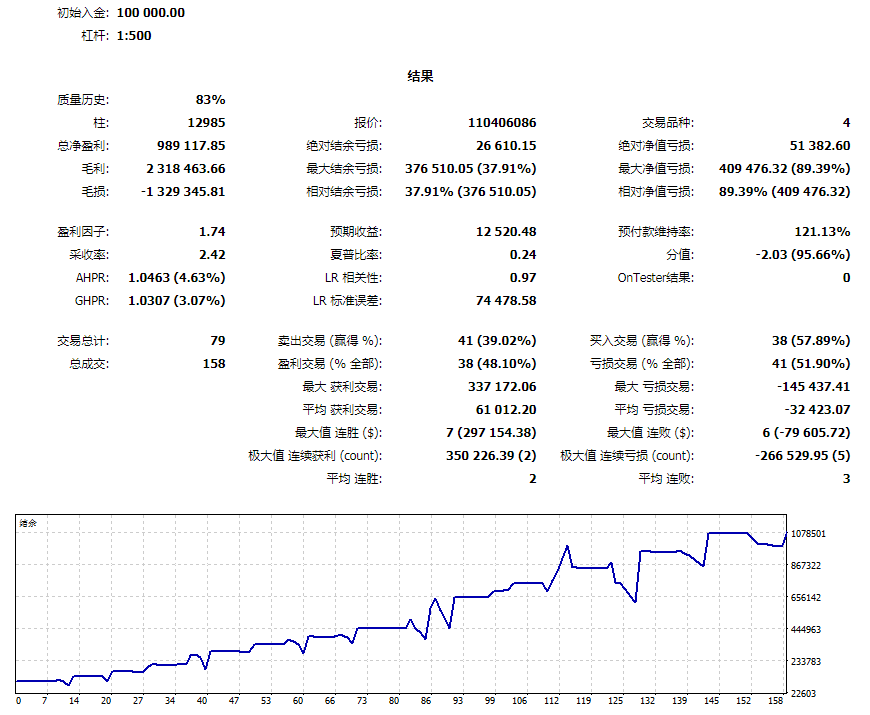
最后来看一下这组四个贵金属的回归测试结果吧,还是按照惯例,我们还是不选取最优参数展示,只是随便找一组普通的参数来做一个展示策略的回测效果。测试时间:2017.01.01 – 2019.03.15,我们看到净值回撤率在89.39%,两年零三个月,收益率在989%。哈哈,看来 IT小哥哥选的这组参数仓位有些重呢。不过我们只看风报比,还是比较不错的。
发表评论