背景

用户反馈：拖动K线图表的时候，自编指标的值会发生变化，如下两图：

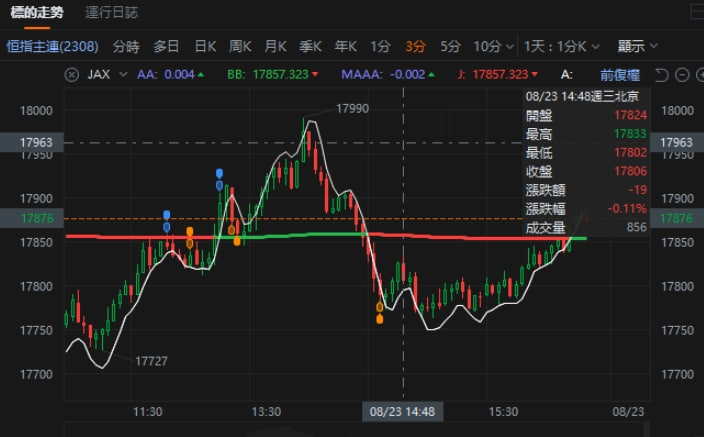
红绿红绿

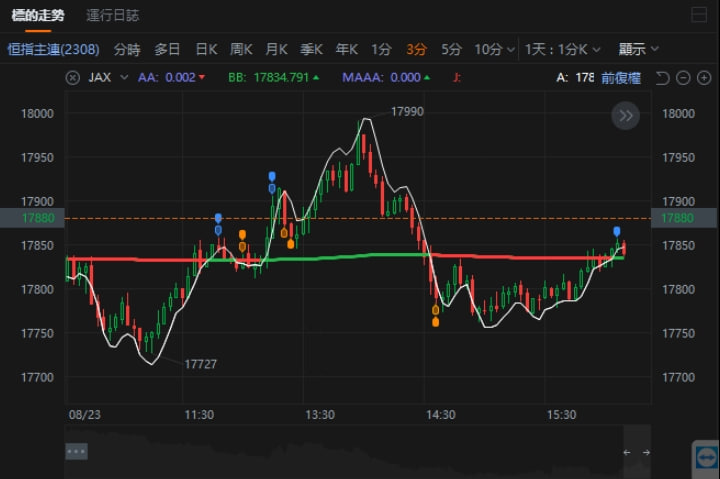
红绿红绿红绿

原因是，他的自编指标用到了 DMA 函数：

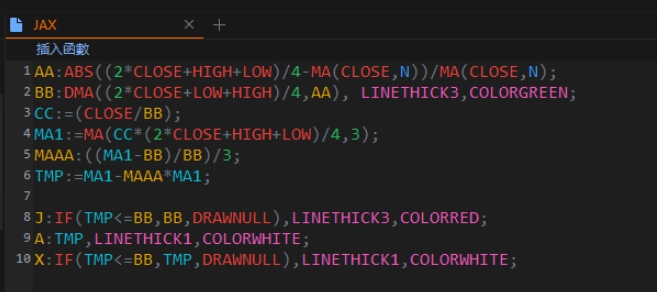
我们来看一下DMA的函数是怎样的：

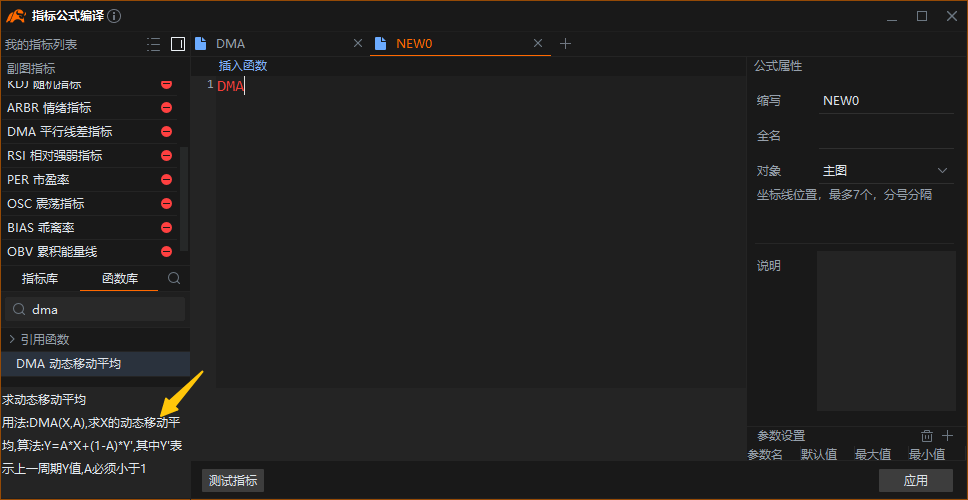
由于每一个值依赖前一个值，递归函数类的指标会受到起始值的干扰。用于计算指标的K线数据集不同，指标的值也会产生差异。

目前用于计算指标的K线数据集缓存的逻辑：

• 图表：PC 图表拖动时，缓存K线和计算指标的逻辑：以图表看得见的左边第一个K线为基准，往前保持至少 1000 个数据点，如果拖动图表导致左边看不见的 K 线数据小于 1000，就会往左边多请求500点。
• 量化：回测和实盘起始（相当于）预留1000根，随着策略的运行，用到的K线数量会越来越多。如果中间碰到公司行动，就会重新恢复到 1000 根。

究竟缓存多少根，才够用户使用，且图表和量化的误差比较小呢？

最简单的等比数列

$$X_{1} = 10$$

$$X_{2} = X_{1}*b1$$

……

$$X_{n} = X_{n-1}*b1$$

0<b1<1，收敛

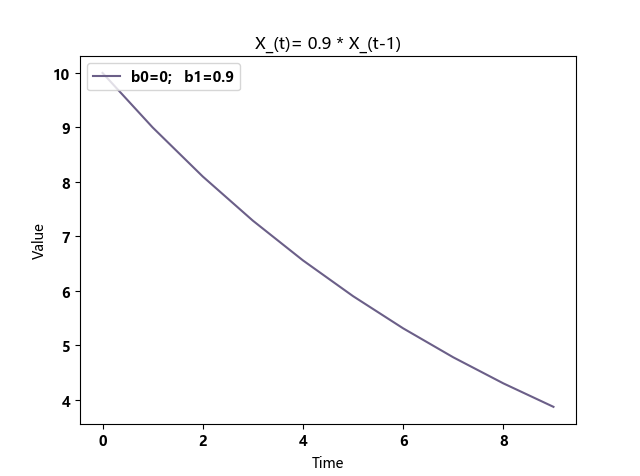
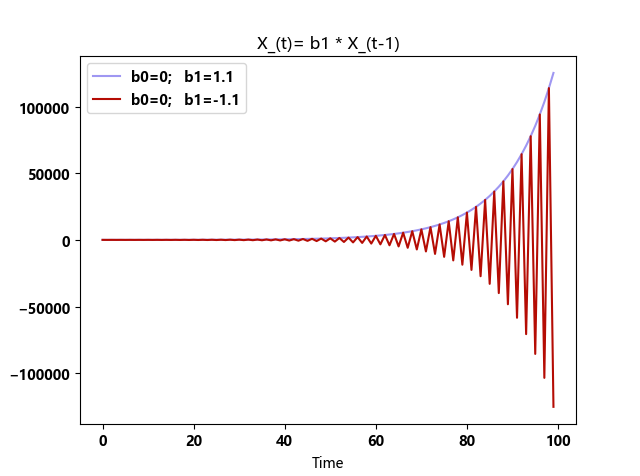
b1>1 或 b1<-1，发散

增加一个变量b0

$$X_{1} = 10$$

$$X_{2} = b0+X_{1}*b1$$

……

$$X_{n} = b0+X_{n-1}*b1$$

b1>1 或 b1<-1，发散

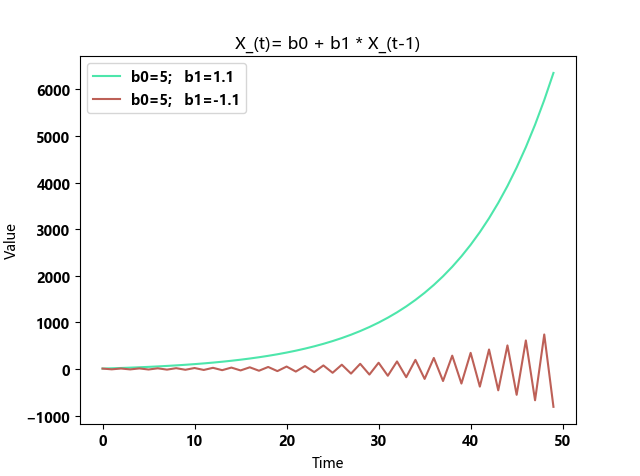
-1<b1<1，均值复归

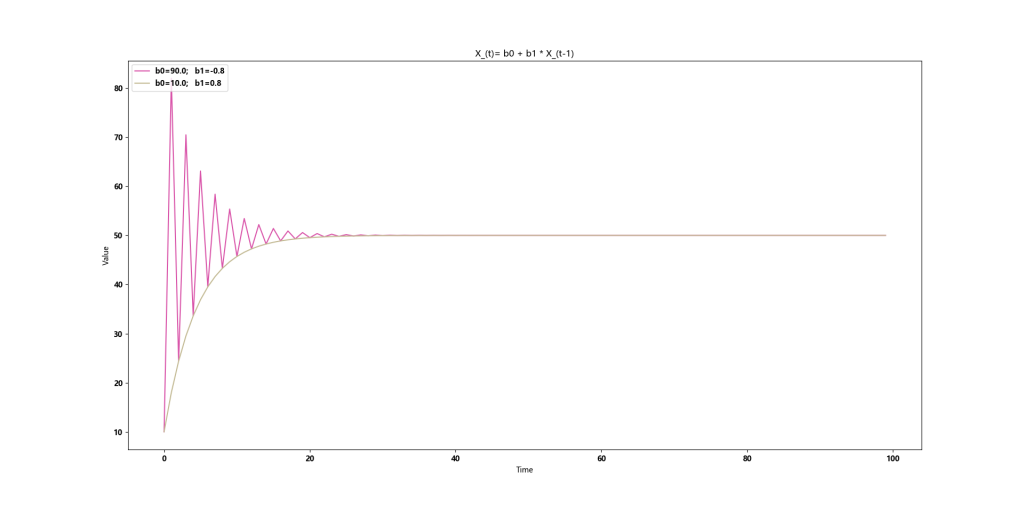
当 b1 为正数时，单向复归，当 b1 为负数时候，震荡复归。

$$复归均值 = \frac{b0}{1-b1}$$

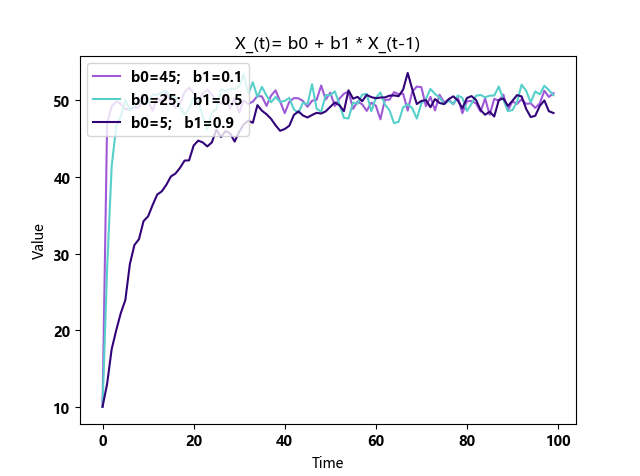
b1与复归速度的关系

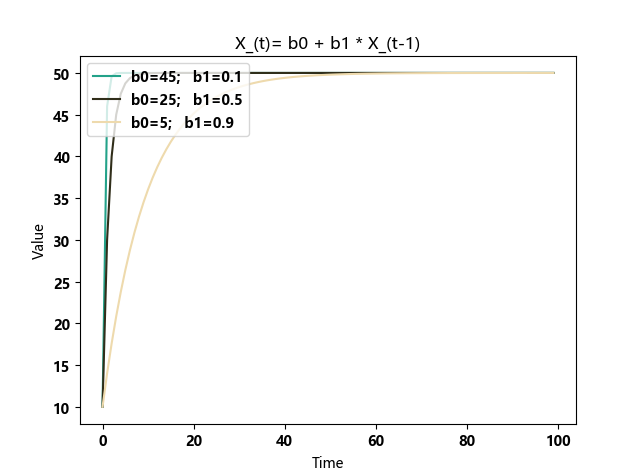
可以看出：当数据量足够的时候，确实可以让结果更快趋于平稳，指标值的误差进入一个比较小的状态。

但是当 b1 无限接近 1 的时候，复归速度也会无限慢。我们无法准备无限的K线用于递归类指标的计算。

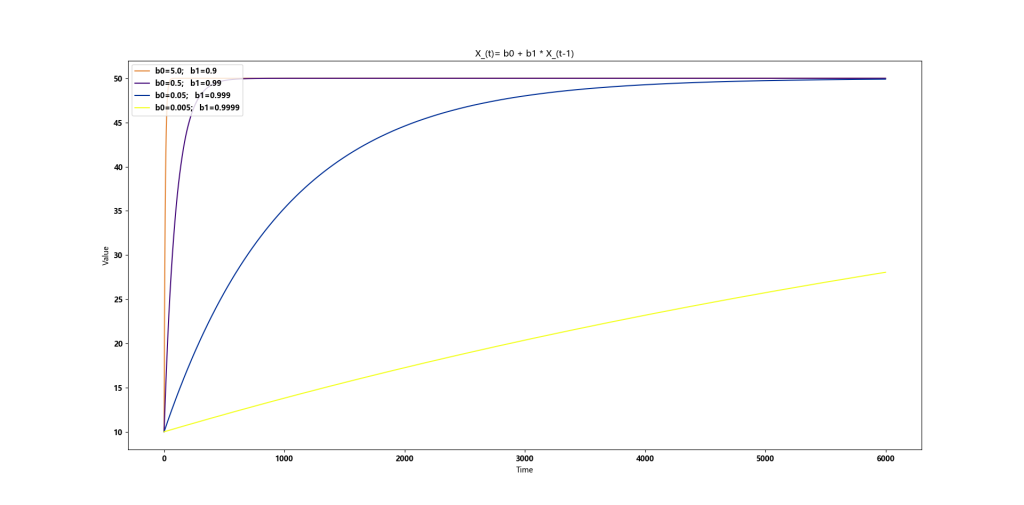
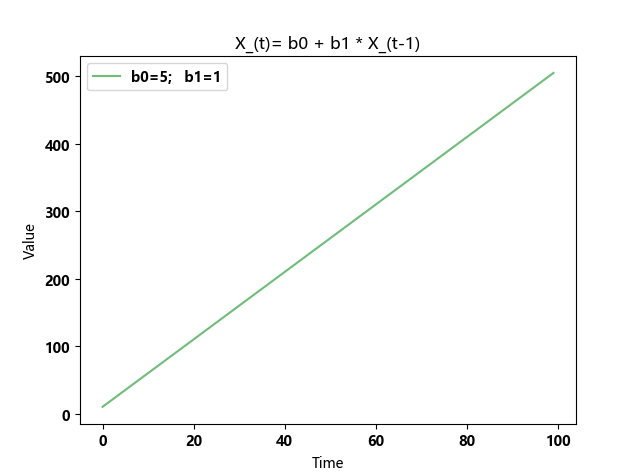
b1=1，等差数列，无法复归

增加一个随机项

$$X_n = b0+b1*X_{n-1}+epsilon$$

b0：常数

b1：自回归系数

epsilon：随机误差，epsilon~N(0,1)

-1<b1<1，均值复归

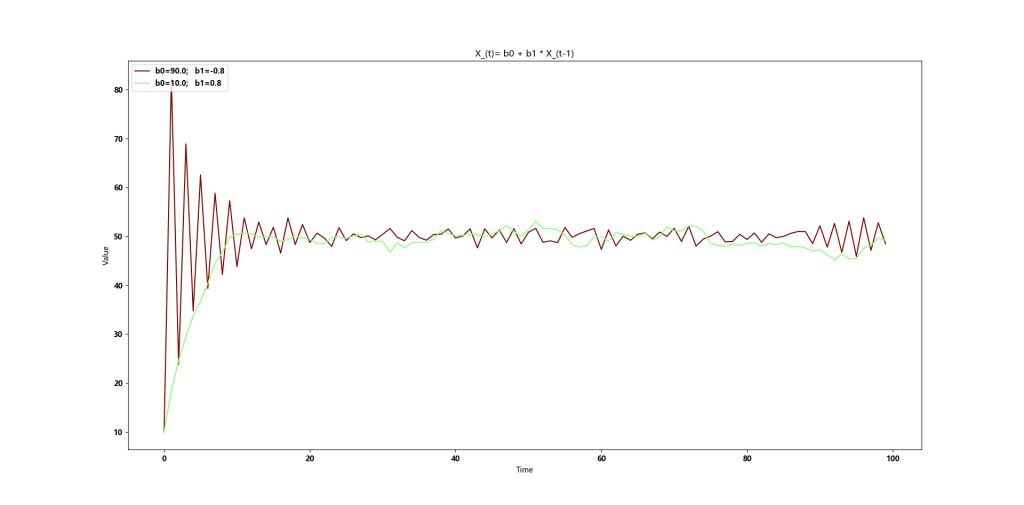
当 b1 为正数时，单向复归，当b1为负数时候，震荡复归。

b1与复归速度的关系

b1与复归后的方差的关系

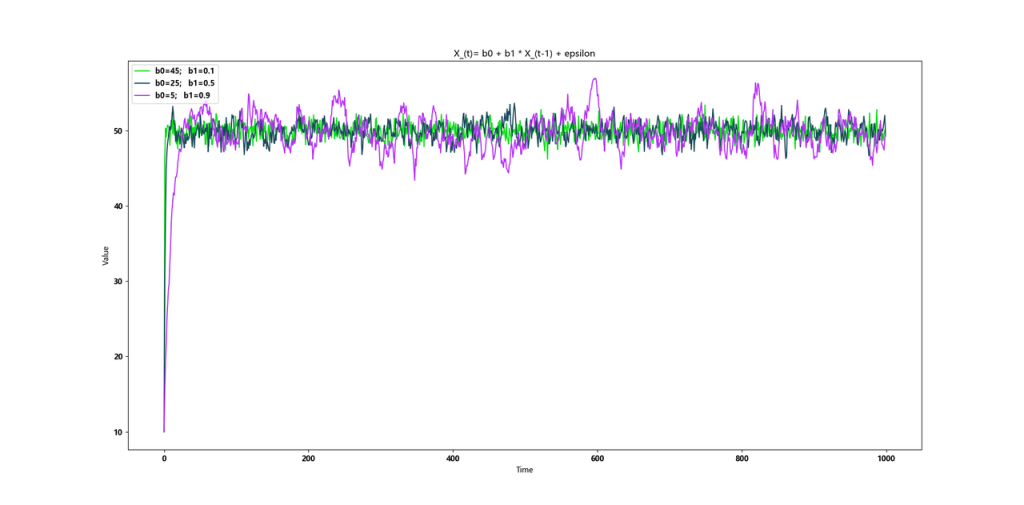
b1无限接近于1时，方差也会无限拉大。

当我们发现拖动图表前后（即用于计算指标的K线数发生变化），指标误差较大时，究竟是源于均值复归速度慢？还是已经复归但方差过大？这也是一个很难判断的事情。

当b0 本身引入随机项的同时，b1趋近于1会放大随机项的影响，导致复归后的方差被拉大。所以简单增加根数并不能保证一定解决问题，观测到误差仍可能很大。

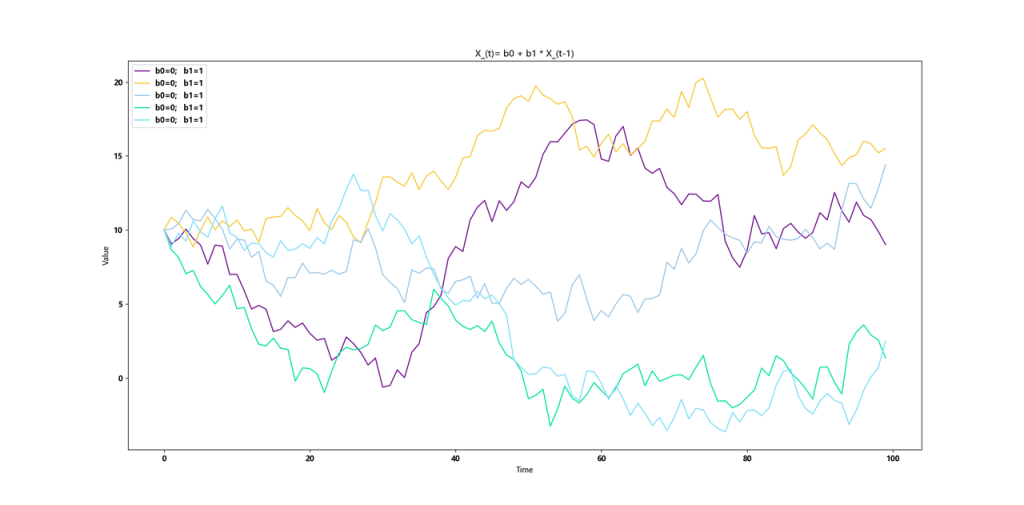
b1=1，随机游走

代码

import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc('font',family='MicroSoft YaHei',weight='bold')  # 设置中文字体

# 定义AR(1)模型的参数
sigma = 1  # 标准差
n = 100  # 样本数


def plot_AR(b1):
    # 生成随机样本
    eps = np.random.normal(loc=0, scale=sigma, size=n)
    # print(eps)
    ar = [10]
    for i in range(1, n):
        ar.append(b1*ar[i-1] + b0 + eps[i])

    # 绘制自回归函数图像
    plt.plot(ar, color=tuple(np.random.rand(3)), label='b0='+str(b0)+';   b1='+str(b1))


if __name__ == '__main__':
    b0 = 5
    plot_AR(b1=0.9)
    plt.title('X_(t)=b0+b1*X_(t-1)+epsilon')  # b1在-1~+1之间都是可以均值复归的
    plt.legend(loc='upper left')
    plt.xlabel('Time')
    plt.ylabel('Value')
    plt.show()