二叉树模型是一个离散时间（discrete-time）模型。

BSM 模型是一个连续时间（continuous-time）模型。

本文主要讲的是应用于股票期权和外汇期权的原始的 BSM 模型。

Black-Sholes-Merton Model

前提

• 期权是欧式期权
• 假设 underlying asset price 服从几何布朗运动（股价服从对数正态分布，股票回报率服从正态分布），且价格是连续波动的（没有跳空缺口）
• 无风险利率是个已知且恒定的
• 资产价格波动率是已知且恒定的
• 市场是无摩擦的
  • 没有交易成本，没有税，没有监管限制
  • 市场是无套利机会的
  • underlying asset 的流动性很高，且连续交易的
  • underlying asset 允许卖空

BSM 模型更适用于股票期权，而不适用于债券期权。原因：

1. 债券临近到期会 pull to par，波动率会放大；

2. 利率是变化的，没有恒定的无风险利率

公式

$$C_{0} = S_{0} \times N(d_{1}) – Ke^{-R_{f}^{c} \times T} \times N(d_{2})$$

$$P_{0} = Ke^{-R_{f}^{c}\times T} \times N(-d_{2}) – S_{0} \times N(-d_{1}) $$

其中，

$$d_{1} = \frac{ln(\frac{S_{0}}{K}) + (R_{f}^{c} + \frac{\sigma ^{2}}{2})T}{\sigma \sqrt{T}}$$

$$d_{2} = d_{1} – \sigma \sqrt{T} = \frac{ln(\frac{S_{0}}{K}) + (R_{f}^{c} – \frac{\sigma ^{2}}{2})T}{\sigma \sqrt{T}} $$

• \(S_{0}\) 是 0 时刻标的资产价格
• K 是行权价格
• T 是期权距离到期日剩余时间（年）
• \(\sigma \) 是标的资产的隐含波动率
• \(R_{f}^{c}\) 是连续复利下的无风险利率
• N(X) 是标准正态分布的累积概率分布函数

tips：累积正态分布函数性质回顾

\( N(-d) = 1 – N(d) \)

公式解读

call & put

由看涨期权的公式，

$$C_{0} = S_{0} \times N(d_{1}) – Ke^{-R_{f}^{c} \times T} \times N(d_{2})$$

我们可以得到：买看涨期权，就相当于买\(N(d_{1})\) 份股票再卖\(N(d_{2})\) 份 T 时刻到期且面值为 K 的零息债券。换句话说，long call 就可以看成是加杠杆买股票（leveraged stock investment）。

由看跌期权的公式，

$$P_{0} = Ke^{-R_{f}^{c}\times T} \times N(-d_{2}) – S_{0} \times N(-d_{1}) $$

买看跌期权，就相当于卖空 \(N(-d_{1})\) 份股票的钱，再买 \(N(-d_{2})\) 份 T 时刻到期且面值为 K 的零息债券。 换句话说，long put 就可以堪称是 long bond 和 short stock 的组合。

\( N(d_{1}) \) & \( N(d_{2}) \)

\( N(d_{1}) \) 就是看涨期权的 Delta

\( -N(-d_{1}) \) 就是看跌期权的 Delta

\( \Delta_{put} = \Delta_{call} – 1 \)

\( N(d_{2}) \) 就是 call 在到期日将会被行权（\( S_{T} > K \)）的 risk-neutral probability（风险中性下的概率）

\( N(- d_{2}) \)就是 put 在到期日将会被行权 （\( S_{T} < K \)） 的 risk-neutral probability（风险中性下的概率）

\( N(d_{2}) + N(- d_{2}) = 1 \)

刚刚我们考虑的都是 Underlying Asset 在持有期间不存在成本 or 收益的，如果考虑到 benefits & costs 又该如何变形呢？

BSM Model with Carrying Benefits or costs

Benefits & Costs

Carry benefits：

• Dividend for stock 股票分红
• Foreign interest rates for currency 外币无风险利率（外汇期权要考虑）

Carry costs：

• Storage costs 储存
• Insurance costs 保险

调整后的公式

这里引入一个新的变量 \(\gamma\)，代表连续时间下的 持有净收益率。

tips：我们用\(S_{0}e^{-\gamma \times T}\) 去代替原公式中所有的\(S_{0}\)

$$C_{0} = S_{0}e^{-\gamma \times T} \times N(d_{1}) – Ke^{-R_{f}^{c} \times T} \times N(d_{2})$$

$$P_{0} = Ke^{-R_{f}^{c}\times T} \times N(-d_{2}) – S_{0}e^{-\gamma \times T} \times N(-d_{1}) $$

其中，

$$d_{1} = \frac{ln(\frac{ S_{0}e^{-\gamma \times T} }{K}) + (R_{f}^{c} + \frac{\sigma ^{2}}{2})T}{\sigma \sqrt{T}}$$

$$d_{2} = d_{1} – \sigma \sqrt{T} = \frac{ln(\frac{ S_{0}e^{-\gamma \times T} }{K}) + (R_{f}^{c} – \frac{\sigma ^{2}}{2})T}{\sigma \sqrt{T}} $$

BSM Model for Options on Currency 外汇期权的 BSM 定价模型

对于外汇期权的 BSM 模型，由于外币和本币都存在无风险收益率，就把外币的无风险收益率当成 \(\gamma\)，而把本币的无风险收益率当成\(R_{f}^{c}\) 即可。

$$C_{0} = S_{0}e^{-R_{foreign} \times T} \times N(d_{1}) – Ke^{-R_{domestic} \times T} \times N(d_{2})$$

BSM Model for Options on Futures 期货期权的 BSM 定价模型

期货期权相关的内容在之前的文章中我们有讲过。

金融工程|衍生品|CFA|期货期权

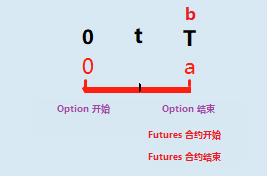
由于期货期权的 underlying 是一张期货合同，期权行权时交割的并不是现货，我们在计算期权行权时（a 时刻）的价值，应该把期货合约到期时（b 时刻）的\(F_{0}(T)\)向前折现到 0 时刻。

tips：我们用\(F_{0}(T)\times e^{-r_{f}^{c}T}\) 去代替原公式中所有的\(S_{0}\)

由上文我们知道，现实中的期货期权 a 时刻和 b 时刻几乎是重合的，重合于 T 时刻。 所以公式中的 T 可以直接取期权的存续时间即可。

由于 \( S_{0}= F_{0}(T)*e^{-r_{f}^{c}\times T} \)，带入基本的 BSM 公式，可以得到期货期权的定价公式：

$$C_{0} = e^{-r_{f}^{c}\times T}\times [F_{0}(T)\times N(d_{1}) – K \times N(d_{2})]$$

$$P_{0} = e^{-r_{f}^{c}\times T}\times [K \times N(- d_{2}) – F_{0}(T)\times N(- d_{1})]$$

其中

$$ d_{1} = \frac{ ln(\frac{F_{0}(T)}{K}) + \frac{\sigma ^{2}}{2}\times T}{\sigma \sqrt{T}} $$

$$ d_{2} = d_{1} – \sigma \sqrt{T} $$

\(\sigma \) 是指与 future price 相关的 valatility。

tips：long call option on futures 就相当于借钱做多期货合约。

BSM Model for Interest Rate Option 利率期权的 BSM 定价公式

利率期权相关的内容在之前的文章《利率期权》中我们有讲过，可以先回顾一下。

金融工程|衍生品|利率期权

如何用 Black Model 给期初的利率期权定价呢？

在《远期利率协议的定价&估值》一文中我们知道，利率的补偿应该用名义本金（NP）和时间来换算成金额：

$$补偿 = NP \times 利差 \times 时间$$

tips：记住：借贷行为的现金流交付是在借贷结束时。

假设在 a 时刻的 a – b 期间的即期利率\(S_{a}(b)\)大于行权价 K， interest rate call option long position 选择行权的话，相当于在 b 时刻流入一笔现金流\(NP\times K \times (b-0)\)，同时在 b 时刻流出一笔现金流 \(NP\times S_{a}(b) \times (b-0)\)。这两笔现金流要从 b 时刻折现到 0 时刻。

而 0 时刻是不知道 a 时刻的即期利率的 \(S_{a}(b)\) ，所以 \(S_{a}\) 要换成站在 0 时刻看 a-b 期间的远期利率 \(FR_{a\times b}\)。

上面我们是假设多方行权的情况，如果考虑上是否行权的概率，就需要用 \(N(d_{1})\) 和 \(N(d_{2})\) 做为系数去调整，得到最终的 Black Model 下的 interest rate option 的定价公式。

$$C_{0} = NP\times e^{-r_{f}^{c}\times \frac{b}{12}}\times [FR_{a\times b}\times N(d_{1}) – K \times N(d_{2})] \times\frac{b-a}{12}$$

$$P_{0} = NP\times e^{-r_{f}^{c}\times \frac{b}{12}}\times [-FR_{a\times b}\times N(-d_{1}) + K \times N(-d_{2})] \times\frac{b-a}{12} $$

tips：\(N(d_{1})\) 中的时间是期权的存续时间 T，也就是图中的 a。