Macaulay Duration 麦考利久期

Macaulay Duration 衡量的是债券现金流的平均回流时间（单位：年）。

$$MacDur = \sum_{t=1}^{n}t \times \frac{PVCF_{t}}{P_{0}} $$

$$P_{0} = \sum PVCF_{t} $$

Amortizing Bond & bullet bond & zero-coupon bond 的麦考利久期特征

zero-coupon bond 由于只有到期日才有现金流，所以距离到期日剩余时间就是其麦考利久期。

bullet bond 由于大部分现金流集中，所以这笔现金流起主导作用。麦考利久期比较大，靠近剩余期限。

Amortizing Bond 的麦考利久期会比较靠近中间，例如等额本息还款，每笔现金流都是一样的，但是前面的现金流的现值更大一些，所以麦考利久期会比剩余期限的一半还短。

投资期限 & 麦考利久期

当投资期限比麦考利久期长，就认为投资期限偏长，再投资风险占主导，利率下行是不利的。

当投资期限比麦考利久期短（提前在市场中卖掉），就认为投资期限偏短，市场价格风险占主导，利率上行是不利的。

当投资期限等于麦考利久期长，就认为再投资风险和市场价格风险相抵消，对利率变动免疫。

Tips：上述条件成立的前提条件：距离下一个付息日之前，利率曲线最多只能动一次，且是 parallel shift（平行移动）。

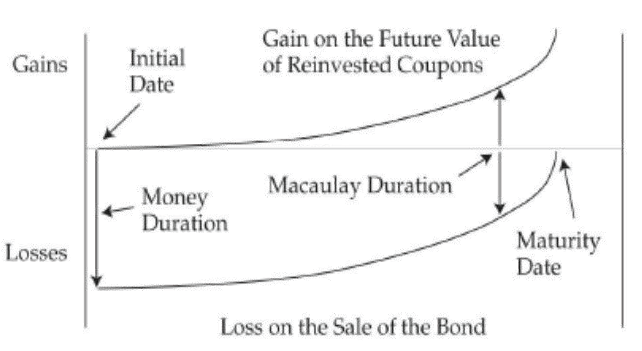
当利率上行时，下图反映的时再投资收益和市场价格损失的关系。

• 在 Macaulay Duration 左边，市场价格损失占主导。
• 在 Macaulay Duration 时间点，再投资收益和市场价格损失相抵消。
• 在 Macaulay Duration 右边，再投资收益占主导。

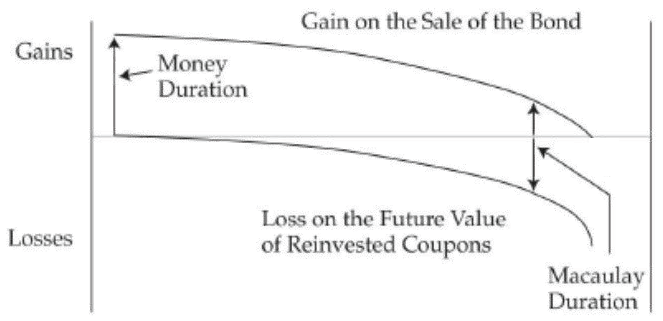
当利率下行时，下图反映的时再投资损失和市场价格利得的关系。

• 在 Macaulay Duration 左边， 市场价格利得占主导。
• 在 Macaulay Duration 时间点， 再投资损失和市场价格利得相抵消。
• 在 Macaulay Duration 右边， 再投资损失占主导。

Duration Gap 久期差

Duration Gap = Macaulay Duration – investment horizon

Tips：上式不要减反了。