看涨期权

European call & American call

欧式看涨期权 和 美式看涨期权 的上下限是一样的。

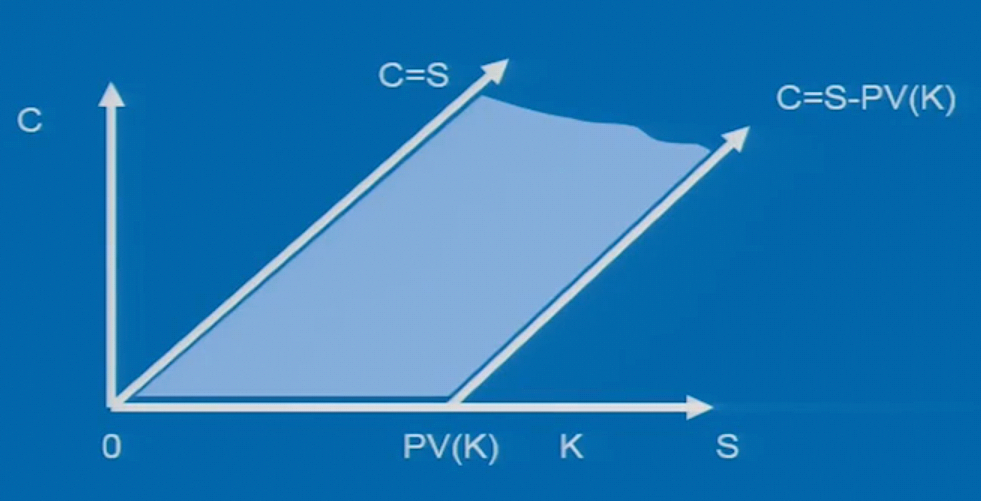
European call & American call 上限

$$C \leq S$$

看涨期权的价格 C 的上限不能超过标的资产的价格 S。

证明方法：反证法

可以通过反证法，设计一个 C > S 的情景，然后发现存在无风险套利的机会。这不符合我们的无套利的前提。

European call & American call 下限

$$ C \geq max[0, S – PV(K)] = max (0, S – Ke^{-rT}) $$

看涨期权的下限不能小于 payoff，也即 \( max(0, S – Ke^{-rT}) \)。

证明方法：组合比较法

构造两个投资组合 portfolio A 和 portfolio B。

portfolio A 和我们之前推导 买卖权平价 的时候构造的 Fiduciary Call 是一样的，由 一份行权价为 K 且到期日为 T 的欧式看涨期权 加 一份票面价值为 K 且到期日为 T 的零息债券 组成。

portfolio A：European Call + \(Ke^{-rT}\)

portfolio B：一份股票

组合名	portfolio A	Portfolio B
组合内容	\(European Call + Ke^{−rT}\)	stock
if \(S_{T}\) ≤ K	0 + K = K	\(S_{T}\)
if \(S_{T}\) ≥ K	\((S_{T} – K) + K = S_{T} \)	\(S_{T}\)

由上表可知：

$$ V_{A} = max ( S_{T}, K ) $$

$$ V_{B} = S_{T} $$

所以在 T 时刻，下式成立：

$$V_{A} \geq V_{B} $$

那么在无套利下，他们在 0 时刻的价值关系也不能反转，否则就存在套利机会。 得到European Call 的下限：

$$call \geq S – Ke^{-rT} $$

$$ call \geq max (0, S – Ke^{-rT}) $$

而理性的 American Call Option holder 是不会选择提前行权的，自然也不会为能提前行权买单。所以在其他条件相同的情况下，American Call 的价格应该等于 European Call 的价格。

看跌期权

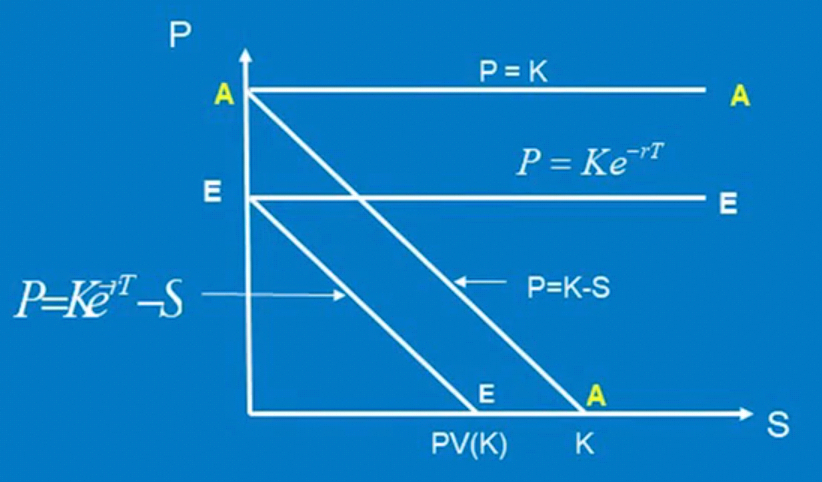
如上图：A-A-A 是美式期权的价格区域，E-E-E 是欧式期权的价格区域。

European Put

European Put 上限

$$ P \leq Ke^{-rT} $$

欧式看跌期权的价格 P 的上限不能超过执行价格 \(Ke^{-rT}\)。

证明方法 ：反证法

可以通过反证法，设计一个 \( P > Ke^{-rT} \) 的情景，然后发现存在无风险套利的机会。这不符合我们的无套利的前提。

European Put 下限

$$ P \geq max(0, Ke^{-rT} – S ) $$

欧式看跌期权的价格 P 的下限不能低于 \( max(0, Ke^{-rT} – S ) \)。

证明方法 ：组合比较法

构造两个投资组合 portfolio C 和 portfolio D。

portfolio C 和我们之前推导 put call parity 的时候构造的 Protective Put 是一样的，由 一份行权价为 K 且到期日为 T 的欧式看跌期权 加 一份股票 组成。

portfolio C：European Put + Stock

portfolio D 是一份票面价值为 K 且到期日为 T 的零息债券。

portfolio D：\(Ke^{-rt}\)

组合名	portfolio C	Portfolio D
组合内容	\(European Put + Stock \)	\( Ke^{-rt} \)
if \(S_{T}\) ≤ K	\((K – S_{T}) + S_{T} = K \)	\( K \)
if \(S_{T}\) ≥ K	\( 0 + S_{T} = S_{T} \)	\( K \)

由上表可知：

$$ V_{C} = max ( S_{T}, K ) $$

$$ V_{D} = K $$

所以在 T 时刻，下式成立：

$$V_{C} \geq V_{D} $$

那么在无套利下，他们在 0 时刻的价值关系也不能反转，否则就存在套利机会。 得到European Call 的下限：

$$ put \geq Ke^{-rT} – S $$

$$ put \geq max (0 , Ke^{-rT} – S) $$

而我们知道，put 的 IV 是\( max (0 , K – S) \)，我们发现当 put 取到下限的时候，期权的价值 \( Ke^{-rT} – S \) 是小于 内在价值 \( K – S \) 的。换句话说，欧式看跌期权是存在时间价值 TV < 0 的情况的。 因此，European put 期限越长，价格不一定越贵。

American Put

American Put 上限

$$ P \leq K $$

美式看跌期权的价格 P 的上限不能超过执行价格 K。

证明方法 ：反证法

可以通过反证法，设计一个 \( P > K \) 的情景，然后发现存在无风险套利的机会。这不符合我们的无套利的前提。

American Put 下限

$$ P \geq max( 0 , K – S ) $$

美式看跌期权的下限就是它的 payoff，也就是内涵价值 IV。

由于 American put 可以提前行权，所以：

美式看跌期权不存在时间价值为负的情况，但是当深度实值的时候存在 TV = 0 的情况。

对于美式看跌期权，当（无股利支付的）标的资产价格下跌到 Time Value = 0 的时候，就应该果断实施，提前拿到钱 $K，就可以在 t – T 期间赚取无风险收益。